द्रवों में तापीय प्रसार

 

 

द्रवों में तापीय प्रसार ठोसों के आयतन प्रसार की भांति ही होता है जिसके लिए आयतन प्रसार का सूत्र भी समान है :-

V = V₀( 1 + γΔT )

द्रवों में अणुओं के बीच बंध, आमतौर पर ठोस पदार्थों की तुलना में दुर्बल होते हैं, इसलिए तापमान में समान वृद्धि के लिए ठोस पदार्थों की तुलना में द्रवों में अधिक तापीय प्रसार होता है।

अतः γ का मान द्रवों के लिए, ठोसों की तुलना में अधिक होता है।

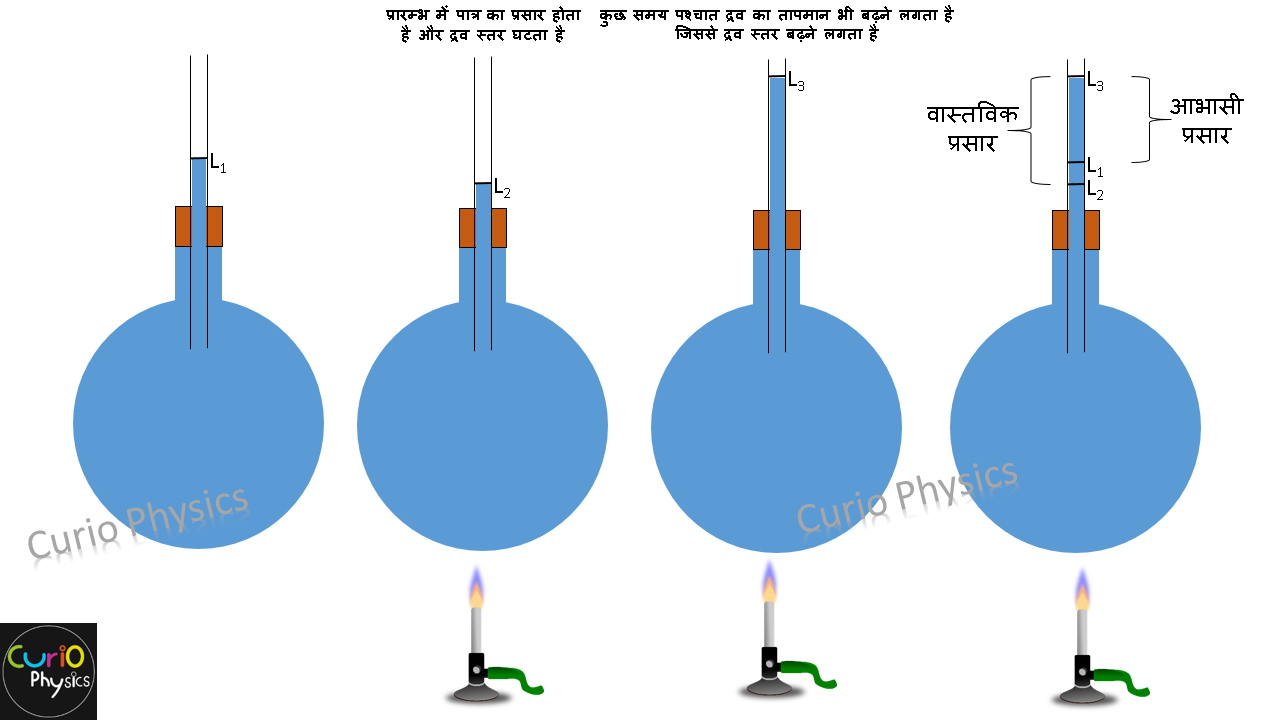
द्रवों को सदैव किसी पात्र में भर कर गर्म किया जाता है अतः प्रारम्भ में निकाय (पात्र + द्रव) को गर्म करने पर पहले पात्र गर्म होता है और प्रसारित होता है जिससे पात्र में द्रव का स्तर गिरता है। किन्तु कुछ समय पश्चात द्रव का तापमान भी बढ़ने लगता है और द्रव का प्रसार, पात्र की तुलना में भी अधिक होता है जिससे द्रव का स्तर बढ़ना प्रारम्भ हो जाता है।

 

अतः द्रवों के दो आयतन प्रसार गुणांक होते हैं :-

1. आभासी प्रसार गुणांक(Coefficient of apparent expansion) γ_a :- जो द्रव के आभासी प्रसार ( वह प्रसार जो प्रतीत होता है, किन्तु वास्तविक नहीं है ) के कारण है। अर्थात वह प्रसार जिस में पात्र के प्रसार पर विचार ना किया जाए।
2. वास्तविक प्रसार गुणांक(Coefficient of real expansion) γ_r :- जो की द्रव के वास्तविक प्रसार के कारण है, अर्थात वह प्रसार जिस में पात्र के प्रसार पर विचार किया जाए।

तर्कसंगत

ΔV_real = ΔV_apparent + ΔV_vessel

V₀ ( γ_real)ΔT = V₀ (γ_apparent)ΔT + V₀ (γ_vessel)ΔT

⇒  γ_real = γ_apparent + γ_vessel

अथवा

γ_r = γ_a + γ_v

जैसा कि हमने देखा, द्रवों का आयतन प्रसार गुणांक γ, सामान्यतया ठोसों की तुलना में अधिक(लगभग 10 गुना) होता है व लगभग सभी द्रव ताप वृद्धि के साथ प्रसारित होते हैं, किन्तु जल इस नियम के लिए एक अपवाद है।

जल का तापीय प्रसार अन्य द्रवों से अलग है। 0ºC से  4ºC तक जल सिकुड़ता है (अर्थात जल का आयतन घटता है व घनत्व बढ़ता है ⇒ 0ºC से 4ºC के मध्य γ ऋणात्मक) और 4ºC के पश्चात तापमान बढ़ने पर जल प्रसारित होता है(अर्थात जल का आयतन बढ़ता  है व घनत्व घटता है)। अतः 4ºC पर जल का घनत्व अधिकतम (1000 kgm^-3) होता है।

अतः 0°C से 4°C के मध्य पानी के इस व्यवहार को जल का अनियमित प्रसार कहते है। जाड़े के दिनों में जब झील की सतह के जल का तापमान 4°C से कम होता है तो इसका घनत्व कम हो जाता है। जिस कारण यह हल्का हो जाता है। इस प्रकार झील की ऊपरी सतह पर बर्फ का जमना प्रारम्भ हो जाता है। जबकि नीचे का जल द्रव अवस्था में रहता है और उसमें रहने वाली मछलियाँ व अन्य जलीय जीव-जन्तु जीवित अवस्था में रहते हैं।

 

उदाहरण :- किसी द्रव का आभासी प्रसार गुणांक 2 पत्रों A व B की सहायता से ज्ञात किया जाता है जो कि क्रमशः γ₁ और γ₂ प्राप्त होता है। यदि पात्र A का रेखीय प्रसार गुणांक α हो तो पात्र B का रेखीये प्रसार गुणांक ज्ञात कीजिये।

हल :- जैसा की हम जानते हैं,    γ_r = γ_a + γ_v

पात्र A के लिए :-

γ_r = γ₁ + γ_v

γ_r = γ₁ + 3α     …..(1)

[क्यूंकि  γ = 3α]

पात्र B के लिए :-

माना पात्र B का रेखीय प्रसार गुणांक x है, तब

γ_r = γ₂ + 3x     …..(2)

समीकरण (1) व (2) से,

γ₁ + 3α = γ₂ + 3x

⇒ x = (γ₁ – γ₂ + 3α)/3

 

उपरोक्त लेख पर वीडियो लेक्चर :-

 

 

Next Topic :- गैसों का तापीय प्रसार

Previous Topic :- विस्तार और संकुचन के कारण धातु पैमाने के पाठ्यांक में त्रुटि