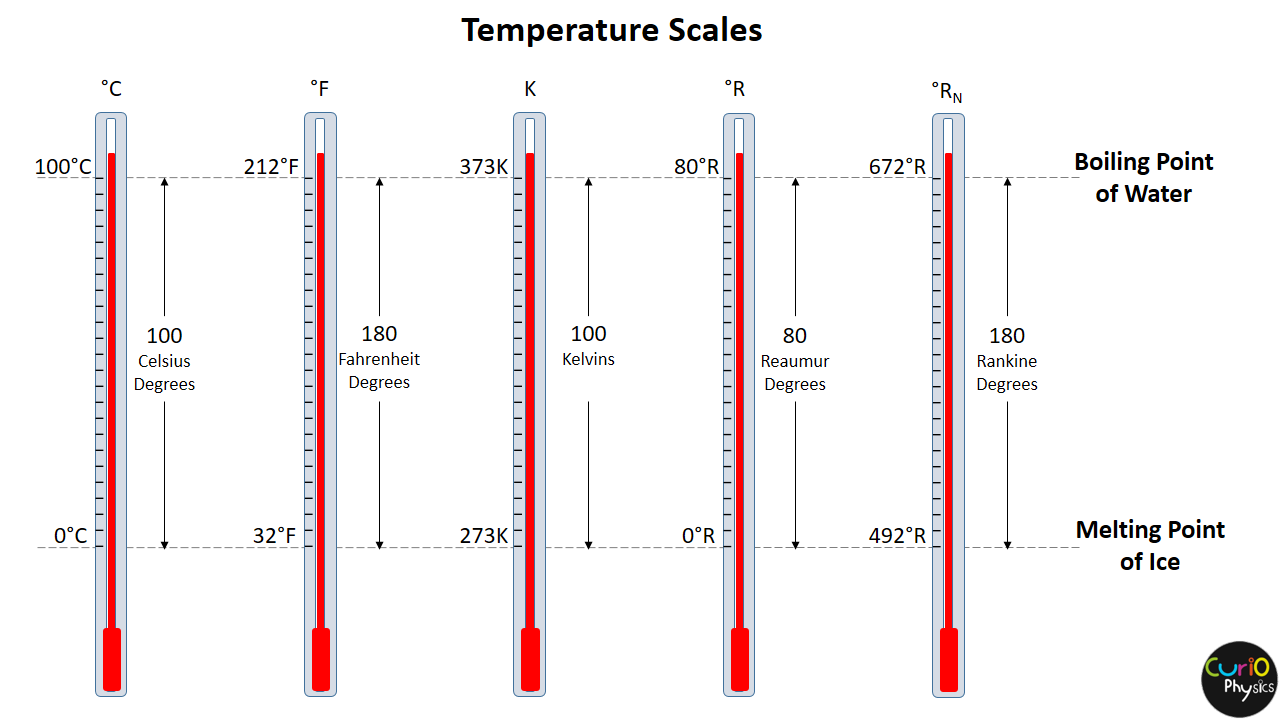
Temperature Scales
Commonly used five temperature scales are :-
- Centigrade / Celsius (ºC)
- Fahrenheit (ºF)
- Kelvin (K)
- Reaumur scale (ºR)
- Rankine Scale (ºRN)
All these scales have Lower Fixed Point (L.F.P.) as melting point of ice and Upper Fixed Point (U.F.P.) as boiling point of water.
All of these temperature scales are having ( U.F.P. – L.F.P. ) number of equal divisions.
(1) Centigrade or celsius scale ( ºC ) :-
This scale was devised by Anders Celsius in the year 1710. In this scale, the interval between the lower fixed point and the upper fixed point is divided into 100 equal parts. Each division on this scale is called one degree centigrade/Celsius (1ºC).
At normal pressure, on this scale :-
Lower Fixed Point (L.F.P.) = 0ºC (melting point of ice )
Upper Fixed Point (U.F.P.) = 100ºC (boiling point of water)
(2) Fahrenheit Scale ( ºF ) :-
This scale was devised by Gabriel Fahrenheit in the year 1717. In this scale, the interval between the lower fixed point and the upper fixed point is divided into 180 equal parts. Each division on this scale is called one degree Fahrenheit (1ºF).
At normal pressure, on this scale :-
Lower Fixed Point (L.F.P.) = 32ºF (melting point of ice )
Upper Fixed Point (U.F.P.) = 212ºF (boiling point of water)
(3) Kelvin scale ( K ) :-
The Kelvin scale was adapted from the Celsius scale in the 19th century by the British scientist William Thompson, later Lord Kelvin. Kelvin was designed in order to set the zero point of the temperature scale at absolute zero(The temperature at which the average kinetic energy of the molecules of a substance becomes zero).Because of this, absolute zero is located at 0 K – Kelvin does not use degrees in its notation. In this scale, the interval between the lower fixed point and the upper fixed point is divided into 100 equal parts. Each division on this scale is called one Kelvin (1K).
At normal pressure, on this scale :-
Lower Fixed Point (L.F.P.) = 273 K (melting point of ice )
Upper Fixed Point (U.F.P.) = 373 K (boiling point of water)
(4) Reaumur Scale ( ºR ) :-
This scale was devised by René Antoine Ferchault de Réaumur (R.A.Reaumur) in the year 1730. In this scale, the interval between the lower fixed point and the upper fixed point is divided into 80 equal parts. Each division on this scale is called one degree Reaumur (1ºR).
At normal pressure, on this scale :-
Lower Fixed Point (L.F.P.) = 0ºR (melting point of ice )
Upper Fixed Point (U.F.P.) = 80ºR (boiling point of water)
(5) Rankine Scale (ºRN) :-
The scale was created by Scottish scientist William John Rankine in the 19th century, shortly after the creation of the Kelvin scale. In this scale, the interval between the lower fixed point and the upper fixed point is divided into 180 equal parts. Each division on this scale is called one degree Rankin (1ºRN).
At normal pressure, on this scale :-
Lower Fixed Point (L.F.P.) = 492ºRN (melting point of ice )
Upper Fixed Point (U.F.P.) = 672ºRN (boiling point of water)
Temperature Scales:-
| Temperature Scale | ºC | ºF | K | ºR | ºRN | Any Scale |
| L.F.P. | 0 | 32 | 273 | 0 | 492 | TL |
| U.F.P. | 100 | 212 | 373 | 80 | 672 | TU |
| Number of Division (N) | 100 | 180 | 100 | 80 | 180 | TU – TL |
All these temperature scales are related to each other by the following relation:-
Temperature increments on these temperature scales are related as :-
Note :-
(1). In general whenever we are to convert temperature from any known scale to unknown scale then we follow the following equation :-
(2). Rise in temperature is same for
- Celsius and Kelvin scale
- Fahrenheit and Rankine Scale
(3). Whenever, ratio of the temperatures has to be taken do not forget to convert the temperatures to absolute Kelvin scale.
For example if we have to find ratio of T1 = 20ºC and T2 = 10ºC, then ratio T1/T2 ≠ 2. Instead the ratio is T1/T2 = (20+273)/(10+273) = 1.035
Example 1. Express a temperature of 60 ºF in degree Celsius and kelvin scale.
Solution. We know that
Now,
T = Tc + 273
⇒ T = 15.55 + 273
⇒ T = 288.55 K
Example 2. An iron piece is heated from 30 ºC to 90 ºC. Find the change in its temperature on Fahrenheit and kelvin temperature scale.
Solution. As,
Now since rise in temperature for both the Celsius and the kelvin scale is the same, so
Example 3. Find at what value of temperature, the reading will be same in the following temperature scales.
- ºF and ºC
- ºC and ºR
- ºC and K
- ºF and ºR
- K and ºR
- K and ºF
Solution.
I.
T – 32 = 1.8 T ⇒ T = -40ºF / -40ºC
II.
This is only possible when T = 0ºC / 0ºR
III.
⇒ T = T-273 ⇒ no solution
IV.
⇒ T = -25.6 ºF / -25.6ºR
V.
⇒ T = -1092 (Not Possible)
On Kelvin temperature scale, a temperature below 0 K is not possible.
⇒ There is not any temperature at which reading on Kelvin and Reaumur temperature scale will be same.
VI.
⇒ T = 574.25K / 574.25ºF
Example 4. A temperature scale ‘x’ is such that the melting point of ice is 50ºx & boiling point of water is 200ºx. Find the reading of scale at a temperature T = 50ºC.
Solution.
Here TC = 50ºC
On solving Tx = 125ºx
Next Topic :- What is Thermal Expansion
Previous Topic :- Measurement of Temperature