Electric Field Intensity
In the previous article The Electric Field Concept we studied about the region around a charge particle, called “Electric Field”. It is the region surrounding a charge (or charge distribution) in which its electrical effects are perceptible. Now In order to explain the strength of ‘action at a distance’, i.e., the strength of ‘force without contact’ between charges we define a term called “Electric Field Intensity”. Electric Field Intensity tells us that how strong the region around a given charge particle is.
There are three methods to define/visualize the strength of electric field :-
- Electric Field Intensity ( A vector function of position
)
- Electric Potential ( A scalar function of position “V” ) and
- Electric Field Lines (A graphical or pictorial representation of electric field).
Our current article is about first method “Electric Field Intensity” so let us study this first.
The concept of test charge
Let us suppose that we have a charge particle Q. Then this charge will obviously modify the space around it and create a region called Electric field. If some other charge particle (positive or negative) brought in this region then that charge particle will experience a force.
Whenever we make a dish or coffee/tea something, and to check how it tastes, we just take a little quantity of it not the whole of it.
Similarly if we want to check the strength of “Electric Field” around a charge particle, then we have to bring another charge particle in that region but that charge particle ( called “TEST CHARGE”) must be of very small magnitude. By taking small test charge we are actually trying, not to disturb the region created by the main charge particle which is being tested. If we take test charge of large magnitude than the main charge, then this will not be a good approach. We will represent that “small magnitude test charge” as q0.
So we can say that test charge q0 is a fictitious charge that is so small in magnitude that it exerts no force on nearby charges but experiences forces due to all of them.
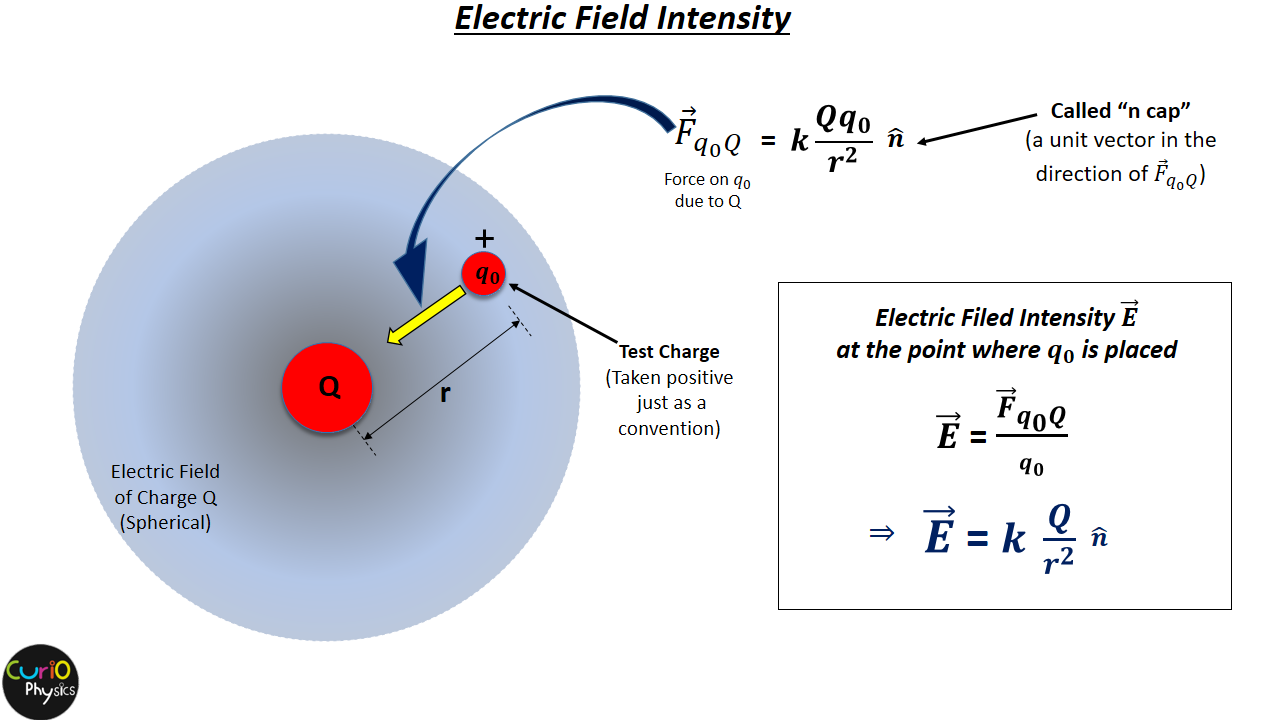
Electric field Intensity due to a point charge
Let in the electric field of charge Q, a test charge q0 enters. Let the distance between the centers of Q and q0 is r. Then using Coulomb’s Law the electrostatic force between Q and q0 is :-
Here is a unit vector in the direction of force
.
Now the electric filed intensity in magnitude and direction at a particular point in the electric field of charge Q is defined as “the force experience by a unit positive test charge placed at that point.”
So according to definition
.
As is a vector quantity, so is
.
If the charge Q is positive then will be directed away from it and if Q is negative then
will be towards Q.
SI unit of electric field intensity is newton/ coulomb (NC-1) or volt/metre(vm-1)
The dimensional formula for E :- [E]=[ MLT-3A-1 ]
In some cases we have to find the force on a given charge particle placed in the electric field of another charge. In that case we turn the equation around and find the force exerted by a known electric field. That is, a charged particle with charge q at a point in space where the electric field is
experiences an electric force :-
If q is positive, the force on the particle is in the direction of and if q is negative then force on it will be in opposite direction of
.
Note :- The electric field intensity is also simply called “electric field”. So the word electric field is used in both sense i.e., to represent the region around a charge particle and also for the intensity of field produced by it.