Continuous Charge Distribution

Spread the love

Continuous Charge Distribution

Introduction :-

The source of Electric Field is either a POINT CHARGE or a CONTINUOUS DISTRIBUTION OF CHARGES.

On microscopic level every material is actually a discontinuous distribution of particles called atoms/molecules, separated by intervening space. Even if we talk about a cup of water(≅250ml), then at microscopic level it is actually a discontinuous distribution of approximately 8.36 x 10²⁴ molecules of water. However if we look at macroscopic level, then the intervening space between atoms/molecules, which is actually very small, can be neglected and the distribution of particles appears to be continuous.

As we know that charge is quantized (properties of electric charge), i.e., charge can exist only as an integral multiple of basic charge (e), therefore, charge distribution is always discrete. But as stated above, at macroscopic level, the distribution of charge particles will also appear to be continuous.

So, when charge particles are continuously distributed over a region, then this is called charge distribution. In other words if “charge is so distributed that the distance between individual charge particles is very small (approaching to zero), then this is called continuous charge distribution.”

Types of Continuous Charge distribution

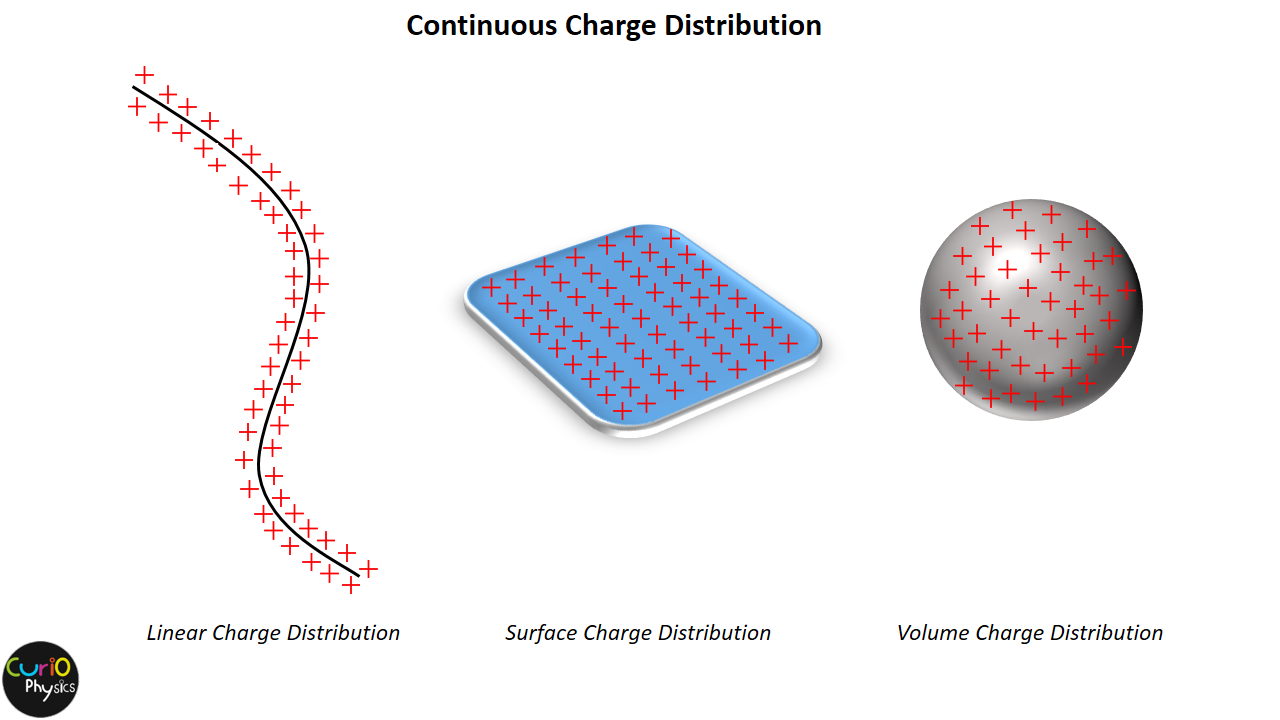
Continuous charge distribution is of three types :-

(1) Linear Charge Distribution (when charge distribution is unidimensional)

When the charge is uniformly distributed over the length of a conductor, then it is called Linear Charge Distribution.

(2) Surface Charge Distribution (when charge distribution is two dimensional)

When the charge is uniformly distributed over the surface of the conductor, it is called Surface Charge Distribution.

(3) Volume Charge Distribution (when charge distribution is three dimensional)

When the charge is distributed over a volume of the conductor, it is called Volume Charge Distribution.

Charge Density for continuous charge distribution

If we consider a small area element (ΔS) of a charged conductor, then this small element is big enough to include a very large number of electrons. Let ΔQ be the total charge on this small area element ΔS. We define Surface Charge Density (σ) at the area element as charge on unit surface area, i.e., $\displaystyle \sigma =\frac{\Delta Q}{\Delta S}$ .

Now according to the type of charge distribution, charge density is also of three types :-

(1) Linear Charge Density (λ) :- If Δl is a small line element of wire on the macroscopic scale that includes a large number of charge particles having a total charge ΔQ then,

$\displaystyle \lambda =\frac{\Delta Q}{\Delta l}$

Unit of λ :- C/m

Dimensions of λ :- [M⁰L^-1TA]

Use :- Linear Charge Density is used in the expressions of charged ring and linear conductors or insulators. For example suppose q charge is uniformly distributed on a circular wire of radius R then linear charge density of the wire $\displaystyle \lambda =\frac{q}{2\pi R}$ .

(2) Surface Charge Density (σ) :- If ΔS is a small area element of a charged conductor on the macroscopic scale that includes a large number of charge particles having a total charge ΔQ then,

$\displaystyle \sigma =\frac{\Delta Q}{\Delta S}$

Unit of σ :- C/m²

Dimensions of σ :- [M⁰L^-2TA]

Use :- Surface Charge Density is used in the expressions of charged disc and infinite charged plates. For example suppose q charge is uniformly distributed on a circular sheet of radius R then surface charge density of the sheet $\displaystyle \sigma =\frac{q}{4\pi {{R}^{2}}}$ .

Note :- σ is maximum on edges of charged rectangular metal plates and vertex of conical charged conductors because at shape edges the area is very small( $\displaystyle \because \sigma \propto \frac{1}{Area}$ ).

(3) Volume Charge Density (ρ) :- If ΔV is a small volume element of a charged conductor on the macroscopic scale that includes a large number of charge particles having a total charge ΔQ then,

$\displaystyle \rho =\frac{\Delta Q}{\Delta V}$

Unit of ρ :- C/m³

Dimensions of ρ :- [M⁰L^-3TA]

Use :- Volume Charge Density is used in the expressions of charged spheres. For example suppose q charge is uniformly distributed inside an insulated sphere of radius R then volume charge density of the sphere $\displaystyle \rho =\frac{q}{\frac{4}{3}\pi {{R}^{3}}}$ .

Continuous Charge Distribution