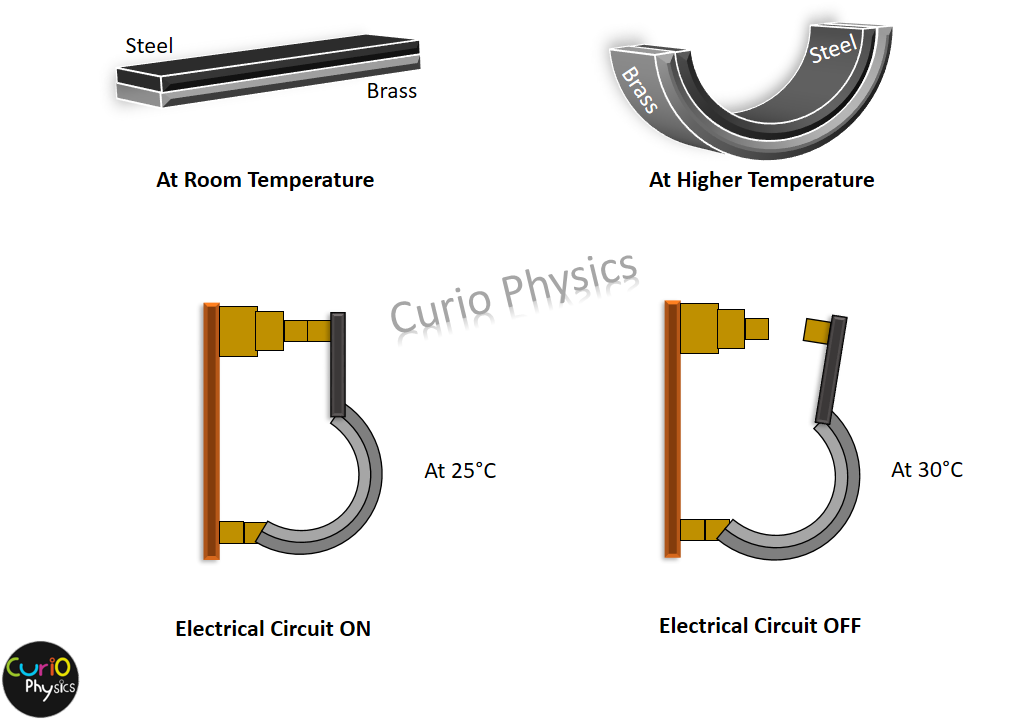
Bimetallic Strip
We know that every metal expands when it is heated, this property of materials is called thermal expansion.
Now the amount of expansion is different for different materials and is determined by a property called coefficient of thermal expansion(γ).
The materials having higher coefficient of thermal expansion than others, expands more for the same rise in temperature. For example brass has high value of coefficient of thermal expansion than steel. So if we have two strips, one of brass and other of steel of same dimensions, then increasing the temperature by same amount of both the strips, the increase in length of brass strip will be more than steel strip.
Bimetallic strip
Two strips, one of steel and other of brass(some times copper) are joined together throughout their length by riveting, brazing or welding(more common). This is called bimetallic strip. Now as the temperature is increased, the increase in length of brass strip is more than steel strip but since they are joined together lengthwise so both the strips bend in the form of an arc.
This property of different amount of expansion of different materials by increase in temperature is utilized in making temperature controlling device called thermostat to make or break electrical contact.
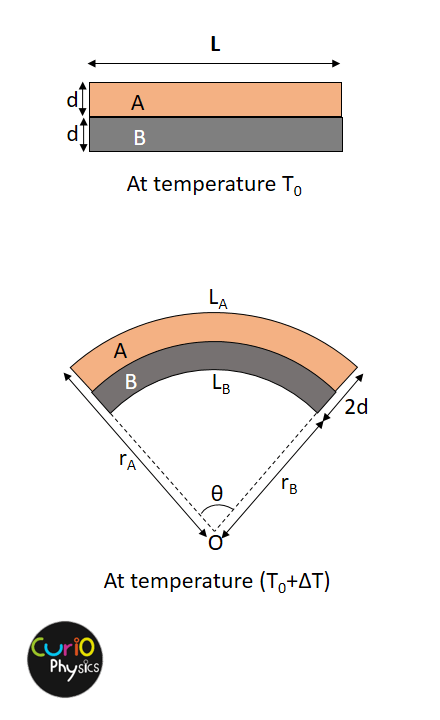
Example :- Two metal strips, each of length L and thickness d at temperature T0 are riveted together so that their ends coincide. One strip is made of metal A having coefficient of linear expansion αA and the other with a coefficient αB , where αA > αB . When this bimetallic strip is heated to a temperature (T0 +ΔT),the bimetallic strip bends into the arc of a circle. Assuming that the thickness 2d of the bimetallic strip remains constant at new temperature, calculate the radius of the circle.
Solution. As αA > αB , hence metal A will be on the outer side and metal B on the inner side of the arc made by bimetallic strip.
New length of strips can be written as
LA = rAθ = L(1 + αAΔT) …..(1)
LB = rBθ = L(1 + αBΔT) …..(2)
Adding eq. (1) and (2), we get
(rA + rB)θ = L [ 2 + (αA + αB)ΔT ]
![\displaystyle \Rightarrow r=\frac{{{r}_{A}}+{{r}_{B}}}{2}=\frac{L[2+({{\alpha }_{A}}+{{\alpha }_{B}})\Delta T]}{2\theta }](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CRightarrow+r%3D%5Cfrac%7B%7B%7Br%7D_%7BA%7D%7D%2B%7B%7Br%7D_%7BB%7D%7D%7D%7B2%7D%3D%5Cfrac%7BL%5B2%2B%28%7B%7B%5Calpha+%7D_%7BA%7D%7D%2B%7B%7B%5Calpha+%7D_%7BB%7D%7D%29%5CDelta+T%5D%7D%7B2%5Ctheta+%7D&bg=ffffff&fg=000&s=0&c=20201002 "Bimetallic Strip 3")
Also from figure :-
rA – rB = 2d …..(4)
From eq.(2) – (1), we get,
θ(rA – rB) = L(αA – αB)ΔT
⇒ θ(2d) = L(αA – αB)ΔT
[from eq. (4) rA – rB = 2d]
Put the value of (5) in Eq. (3) :-
![\displaystyle \Rightarrow r=\frac{L[2+({{\alpha }_{A}}+{{\alpha }_{B}})\Delta T]2d}{2L({{\alpha }_{A}}-{{\alpha }_{B}})\Delta T}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CRightarrow+r%3D%5Cfrac%7BL%5B2%2B%28%7B%7B%5Calpha+%7D_%7BA%7D%7D%2B%7B%7B%5Calpha+%7D_%7BB%7D%7D%29%5CDelta+T%5D2d%7D%7B2L%28%7B%7B%5Calpha+%7D_%7BA%7D%7D-%7B%7B%5Calpha+%7D_%7BB%7D%7D%29%5CDelta+T%7D&bg=ffffff&fg=000&s=0&c=20201002 "Bimetallic Strip 6")
![\displaystyle \Rightarrow r=\frac{[2+({{\alpha }_{A}}+{{\alpha }_{B}})\Delta T]d}{({{\alpha }_{A}}-{{\alpha }_{B}})\Delta T}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CRightarrow+r%3D%5Cfrac%7B%5B2%2B%28%7B%7B%5Calpha+%7D_%7BA%7D%7D%2B%7B%7B%5Calpha+%7D_%7BB%7D%7D%29%5CDelta+T%5Dd%7D%7B%28%7B%7B%5Calpha+%7D_%7BA%7D%7D-%7B%7B%5Calpha+%7D_%7BB%7D%7D%29%5CDelta+T%7D&bg=ffffff&fg=000&s=0&c=20201002 "Bimetallic Strip 7")
Previous Topic :- Effect of Temperature on Upthrust