द्विधातु पट्टी(Bimetallic strip)
का थर्मोस्टैट्स में प्रयोग
हम जानते हैं कि हर धातु गर्म होने पर प्रसारित होती है, पदार्थों के इस गुण को तापीय प्रसार कहा जाता है।
अब प्रसार की मात्रा विभिन्न पदार्थों के लिए अलग-अलग होती है और यह पदार्थों के गुण, तापीय प्रसार गुणांक (γ) द्वारा निर्धारित की जाती है।
जिन पदार्थों का तापीय प्रसार गुणांक (γ) अधिक होता है, वे अन्य पदार्थों की तुलना में समान तापान्तर के लिए अधिक प्रसारित होते हैं। उदाहरण के लिए पीतल(brass) का तापीय प्रसार गुणांक, इस्पात(steel) के तापीय प्रसार गुणांक की तुलना में अधिक होता है। इसलिए यदि हमारे पास दो पट्टियां हों, एक पीतल की और एक स्टील की जिनके आयाम समान हों, तो दोनों पट्टियों का समान मात्रा में तापमान बढ़ाने पर, पीतल की पट्टी की लंबाई में वृद्धि, स्टील की पट्टी की लंबाई में वृद्धि से अधिक होगी।
द्विधातु पट्टी(Bimetallic strip) :-
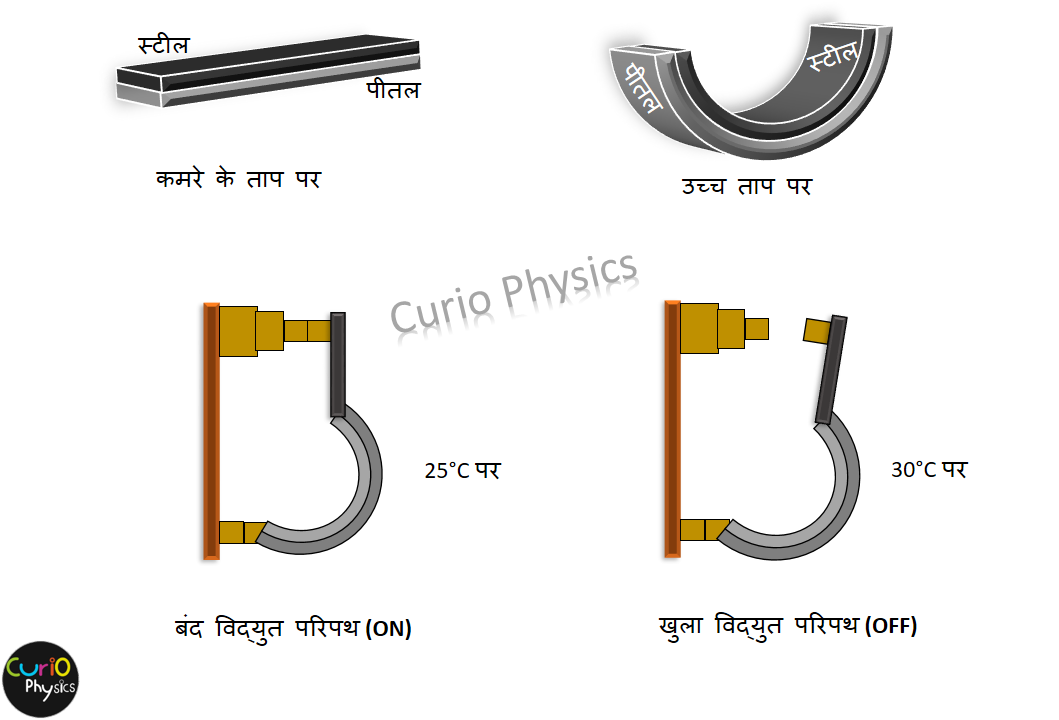
दो पट्टियां, एक स्टील की और दूसरी पीतल की(अथवा तांबे की), इन्हे इनकी लंबाई के अनुदिश जोड़कर(रिवाइटिंग, ब्रेज़िंग या वेल्डिंग द्वारा) बनी पट्टिका को द्विधात्वीय पट्टी कहा जाता है। अब जैसे-जैसे तापमान बढ़ता है, पीतल की पट्टी की लंबाई में वृद्धि, स्टील की पट्टी से अधिक होती है लेकिन चूंकि दोनों पट्टियां लंबाई के अनुदिश जुड़ि हैं, इसलिए दोनों पट्टियां एक चाप के रूप में मुड़ जाती हैं।
तापमान में वृद्धि से विभिन्न धातुओं के अलग-अलग विस्तार के इस गुण का उपयोग विद्युत संपर्क बनाने या तोड़ने के लिए थर्मोस्टेट नामक तापमान नियंत्रक उपकरण बनाने में किया जाता है।
उदाहरण :
दो धातु की पट्टियां, प्रत्येक की लंबाई L और मोटाई d को T0 तापमान पर एक साथ जोड़ा जाता है ताकि उनके सिरों का संयोग हो। एक पट्टी धातु A से बनी है जिसका रैखिक प्रसार गुणांक αA है और दूसरी पट्टी धातु B से बनी है जिसका रैखिक प्रसार गुणांक αB है, जहाँ αA > αB है। जब इस द्विधातु पट्टी को तापमान (T0 + ΔT) तक गर्म किया जाता है, तो द्विधातु पट्टी एक वृत्त के चाप के रूप में मुड़ जाती है। यह मानते हुए कि द्विधातु पट्टी की मोटाई 2d नए तापमान पर नियत रहती है, चाप की त्रिज्या की गणना करें।
हल :-
क्यूंकि αA > αB , अतः धातु A द्विधातु पट्टी द्वारा बनाई गई चाप के बाहरी तरफ होगी और धातु B चाप के अंदरूनी तरफ होगी।
पट्टियों की नई लम्बाई इस प्रकार लिखी जा सकती है :-
LA = rAθ = L(1 + αAΔT) …..(1)
LB = rBθ = L(1 + αBΔT) …..(2)
समीकरण (1) व (2) को जोड़ने पर,
(rA + rB)θ = L [ 2 + (αA + αB)ΔT ]
…..(3)
चित्र से :-
rA – rB = 2d …..(4)
समीकरण (1) – (2) से,
θ(rA – rB) = L(αA – αB)ΔT
⇒ θ(2d) = L(αA – αB)ΔT
[समीकरण (4) से, rA – rB = 2d]
…..(5)
समीकरण (5) का मान समीकरण (3) में रखने पर :-
उपरोक्त लेख का विडियो लेक्चर :-
Previous Topic :- उत्प्लावन बल पर तापमान का प्रभाव