तापमान पैमाने
सामान्यतया प्रयोग किये जाने वाले पांच तापमान पैमाने निम्न हैं :-
- सेल्सियस / सेंटीग्रेड (ºC)
- फ़ारेनहाइट (ºF)
- केल्विन (K)
- रोमर (ºR)
- रैंकिन (ºRN)
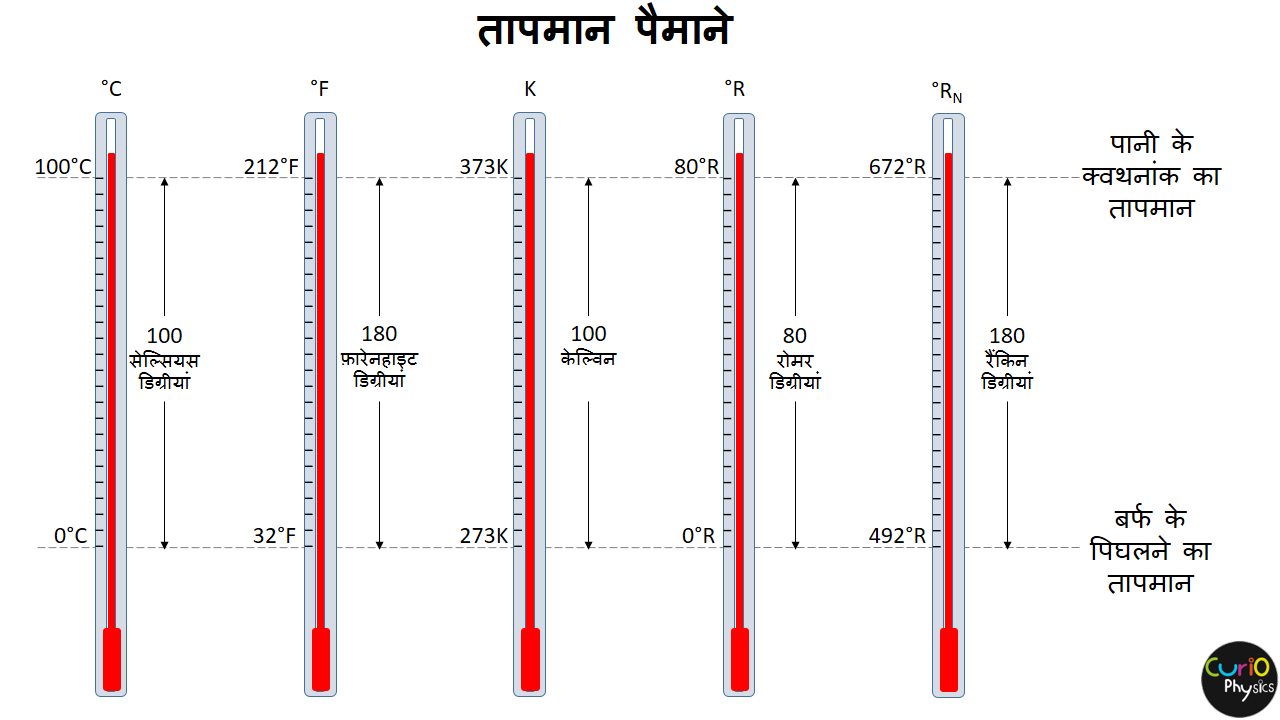
इन सभी पैमानों में बर्फ के पिघलने के तापमान को, निम्नतम नियत बिंदु (L.F.P.) और जल के क्वथनांक के तापमान को उच्चतम नियत बिंदु (U.F.P.) बिंदु के रूप में लिया जाता है।
इन सभी पैमानों में (U.F.P. – L.F.P.) की एक निश्चित संख्या होती है।
(1) सेल्सियस / सेंटीग्रेड (ºC) :-
यह पैमाना वर्ष 1710 में एंडर्स सेल्सियस द्वारा तैयार किया गया था। इस पैमाने में, निम्नतम नियत बिंदु (L.F.P.) और उच्चतम नियत बिंदु (U.F.P.) के बीच के अंतराल को 100 बराबर भागों में विभाजित किया जाता है। इस पैमाने पर प्रत्येक विभाजन को एक डिग्री सेल्सियस / सेंटीग्रेड (1ºC) कहा जाता है।
सामान्य दाब पर, इस पैमाने में : –
निम्नतम नियत बिंदु (L.F.P.) = 0ºC ( बर्फ के पिघलने का तापमान )
उच्चतम नियत बिंदु (U.F.P.) = 100ºC ( जल के क्वथनांक का तापमान )
(2) फ़ारेनहाइट ( ºF ) :-
इस पैमाने को गेब्रियल फारेनहाइट ने वर्ष 1717 में तैयार किया था। इस पैमाने में, निम्नतम नियत बिंदु (L.F.P.) और उच्चतम नियत बिंदु (U.F.P.) के बीच के अंतराल को 180 बराबर भागों में विभाजित किया जाता है। इस पैमाने पर प्रत्येक विभाजन को एक डिग्री फ़ारेनहाइट (1ºF) कहा जाता है।
सामान्य दाब पर, इस पैमाने में : –
निम्नतम नियत बिंदु (L.F.P.) = 32ºF ( बर्फ के पिघलने का तापमान )
उच्चतम नियत बिंदु (U.F.P.) = 212ºF ( जल के क्वथनांक का तापमान )
(3) केल्विन (K) :-
कैल्विन पैमाना को 19 वीं शताब्दी में ब्रिटिश वैज्ञानिक विलियम थॉम्पसन, बाद में लॉर्ड केल्विन द्वारा सेल्सियस पैमाने को रूपांतरित करके बनाया गया था। केल्विन को तापमान के शून्य बिंदु को निरपेक्ष शून्य( वह तापमान जिस पर किसी पदार्थ के अणुओं की औसत गतिज ऊर्जा शून्य हो जाए) पर सेट करने के लिए डिज़ाइन किया गया था। इसके कारण, पूर्ण शून्य 0 K पर स्थित है – केल्विन अपने अंकन में डिग्री का उपयोग नहीं करता है। इस पैमाने में, निम्नतम नियत बिंदु (L.F.P.) और उच्चतम नियत बिंदु (U.F.P.) के बीच के अंतराल को 100 बराबर भागों में विभाजित किया जाता है। इस पैमाने पर प्रत्येक विभाजन को एक कैल्विन (1K) कहा जाता है।
सामान्य दाब पर, इस पैमाने में : –
निम्नतम नियत बिंदु (L.F.P.) = 273 K ( बर्फ के पिघलने का तापमान )
उच्चतम नियत बिंदु (U.F.P.) = 373 K ( जल के क्वथनांक का तापमान )
(4) रोमर (ºR) :-
इस पैमाने को वर्ष 1730 में रेने एंटोनी फेरचॉल्ट डी रेयूमुर (R.A.Reaumur) द्वारा तैयार किया गया था। इस पैमाने में, निम्नतम नियत बिंदु (L.F.P.) और उच्चतम नियत बिंदु (U.F.P.) के बीच के अंतराल को 80 बराबर भागों में विभाजित किया जाता है। इस पैमाने पर प्रत्येक विभाजन को एक डिग्री रेयूमुर (1ºR) कहा जाता है।
निम्नतम नियत बिंदु (L.F.P.) = 0 ºR ( बर्फ के पिघलने का तापमान )
उच्चतम नियत बिंदु (U.F.P.) = 80 ºR ( जल के क्वथनांक का तापमान )
(5) रैंकिन (ºRN) :-
इस स्केल का निर्माण स्कॉटिश वैज्ञानिक विलियम जॉन रैंकिन द्वारा 19 वीं शताब्दी में केल्विन स्केल के निर्माण के कुछ समय बाद किया गया था। इस पैमाने में, निम्नतम नियत बिंदु (L.F.P.) और उच्चतम नियत बिंदु (U.F.P.) के बीच के अंतराल को 180 बराबर भागों में विभाजित किया जाता है। इस पैमाने पर प्रत्येक विभाजन को एक डिग्री रैंकिन (1ºRN) कहा जाता है।
निम्नतम नियत बिंदु (L.F.P.) = 492 ºRN ( बर्फ के पिघलने का तापमान )
उच्चतम नियत बिंदु (U.F.P.) = 672 ºRN ( जल के क्वथनांक का तापमान )
तापमान पैमाने :-
| तापमान पैमाना | ºC | ºF | K | ºR | ºRN | अन्य पैमाना |
| L.F.P. | 0 | 32 | 273 | 0 | 492 | TL |
| U.F.P. | 100 | 212 | 373 | 80 | 672 | TU |
| भागों के संख्या (N) | 100 | 180 | 100 | 80 | 180 | TU – TL |
ये सभी तापमान पैमाने निम्नलिखित सम्बन्ध द्वारा एक दूसरे से संबंधित हैं :-
इन पैमानों पर तापमान वृद्धि निम्नानुसार संबंधित है: –
नोट:-
(1). सामान्य तौर पर जब भी हम किसी ज्ञात तापमान पैमाने से तापमान को अज्ञात तापमान पैमाने पर बदलते हैं तो हम निम्नलिखित समीकरण का पालन करते हैं : –
(2). निम्न पैमानों पर तापान्तर समान है:-
- सेल्सियस और केल्विन
- फ़ारेनहाइट और रैंकिन
(3). जब भी, तापमान का अनुपात लेना हो, तो तापमान को केल्विन पैमाने पर बदलना ना भूलें ।
उदाहरण के लिए यदि हमें T1 = 20ºC और T2 = 10 ºC का अनुपात ज्ञात करना है, तो T1/T2 ≠ 2 । इसके बजाय अनुपात T1 / T2 = (20 + 273) / (10 + 273) =1.035 होगा।
उदाहरण 1:- 60 ºF के तापमान को, डिग्री सेल्सियस और केल्विन स्केल में व्यक्त करें।
हल:- हम जानते हैं की –
अब
T = Tc + 273
⇒ T = 15.55 + 273
⇒ T = 288.55 K
उदाहरण 2:- एक लोहे के टुकड़े को 30 ºC से 90 ºC तक गर्म किया जाता है। फ़ारेनहाइट और केल्विन तापमान पैमाने के लिए इसके तापमान में परिवर्तन ज्ञात करें।
हल:- क्यूंकि
अब चूंकि सेल्सियस और केल्विन पैमाने दोनों के लिए तापमान में वृद्धि समान होती है, इसलिए
उदाहरण 3:- नीचे कुछ तापमान पैमाने दिए गए हैं, इन के लिए वह तापमान ज्ञात कीजिये जिस पर पाठ्यांक समान आए।
- ºF और ºC
- ºC और ºR
- ºC और K
- ºF और ºR
- K और ºR
- K और ºF
हल:-
I.
T – 32 = 1.8 T ⇒ T = -40ºF / -40ºC
II.
यह केवल तभी संभव है जब T = 0ºC / 0ºR
III.
⇒ T = T-273 ⇒ कोई हल नहीं
IV.
⇒ T = -25.6 ºF / -25.6ºR
V.
⇒ T = -1092 (सम्भव नहीं)
केल्विन पैमाने पर 0 K से नीचे का तापमान नहीं होता।
⇒ ऐसा कोई तापमान नहीं है , जिस पर केल्विन और रेयूमुर तापमान पैमाने पर तापमान समान हो ।
VI.
⇒ T = 574.25K / 574.25ºF
उदाहरण 4:- एक पैमाना ‘x’ इस प्रकार है कि इस पर बर्फ के पिघलने का तापमान 50ºx व जल का क्वथनांक 200ºx है। 50ºC तापमान पर पैमाने का पाठ्यांक ज्ञात कीजिये।
हल:-
यहाँ TC = 50ºC
हल करने पर Tx = 125ºx
उपरोक्त लेख “तापमान पैमाने” का वीडियो लेक्चर :-
Next Topic :- तापीय प्रसार
Previous Topic :- ताप मापन का सिद्धांत


Nice sir thanks so much
Thank you so much sir nice 💟💟
nice guru ji